La capitalizzazione ad interesse composto è uno dei concetti più importanti nella matematica finanziaria, se non il più importante.
La caratteristica fondamentale di questo regime di capitalizzazione è che il capitale investito genera interessi durante tutto il periodo di riferimento e che tali interessi maturati vengono incorporati al capitale iniziale, generando quindi ulteriori interessi nei periodi successivi.
In pratica non è soltanto il capitale iniziale a generare interessi (come accadeva con l’interesse semplice) ma anche l’interesse già maturato concorre a generare altri interessi.
Conseguentemente, il montante generato alla fine di ogni periodo di riferimento diventa il “capitale” su cui si generano gli interessi nel periodo successivo. Ne deriva quindi che il montante non cresce più in maniera proporzionale (come per l’interesse semplice), bensì in maniera esponenziale.
Proviamo a capire meglio, con l’ausilio di formule, grafici ed esempi.
Formule
A differenza dell’interesse semplice, dobbiamo qui scomporre la formula negli n periodi che compongono l’operazione.
Indichiamo con M1 il montante generato alla fine del primo periodo di riferimento:
M1 = C + (C * i) = C (1 + i)
Sulla base di quanto detto precedentemente, M1 diventa quindi la base su cui si generano gli interessi del periodo successivo, ovvero M2. Di conseguenza:
M2 = M1 + (i * M1) = M1 * (1 + i) = C * (1+ i) * (1 + i) = C (1 + i )2
e:
M3 = M2 + (i * M2) = M2 * (1 + i) = C (1 + i )2 * (1 + i) = C (1 + i)3
Ripetendo la medesima operazione ipotizzando n periodi ne consegue che:
Mn = Mn-1 + (i * Mn-1) = Mn-1 * (1 + i) = C (1 + i )n-1 * (1 + i) = C (1 + i)n
Pertanto la formula di calcolo del montante nel regime di capitalizzazione ad interesse composto diventa:
Mt = C (1 + i)t
Conseguentemente l’interesse (I = M – C) si calcola come:
It = C (1 + i)t – C = C [(1 + i)t – 1]
Facciamo 2 esempi. I numeri aiutano sempre a capire meglio.
1- Ipotizziamo di prestare ad un amico un capitale C pari a 100 Euro (C=100), per un tempo t pari ad un anno (t=1), ad un tasso di interesse i pari all’1% annuo (i=0,01).
Sostituendo questi valori nelle formula precedenti otteniamo che:
M = 100 (1 + 0,01)1 = 100 (1,01) = 101
I = 100 * [(1 + 0,01)1 – 1] = 100 * 0,01 = 1
Vediamo che in questo specifico esempio (in cui n=1) il montante generato dalla capitalizzazione semplice (esempio 1 a questo link) e da quella composta si equivalgono. Sarà sempre così? Vediamo ulteriori esempi.
2- Ipotizziamo questa volta di prestare ad un amico un capitale C pari a 1.000 Euro (C=1.000), per un periodo di tempo pari a 4 anni (t=4), ad un tasso di interesse i del 2% annuo (i=0,02).
Sostituendo questi valori nelle formula precedenti otteniamo che:
M = 1000 (1 + 0,02)4 = 1000 (1,08243216) = 1.082,43216
I = 1000 * [(1 + 0,02)4 – 1] = 82,43216
Vediamo dunque che in questo esempio (in cui n > 1) il montante generato dalla capitalizzazione composta è maggiore di quello generato nella capitalizzazione semplice (esempio 2 a questo link).
Confronto tra i montanti nella capitalizzazione semplice e nella capitalizzazione composta
Ma quindi quale tra i due sistemi genera un montante maggiore, la capitalizzazione semplice o la capitalizzazione composta? Confrontiamo esempi con durate diverse nel caso in cui C = 10.000 ed i = 5% annuo.
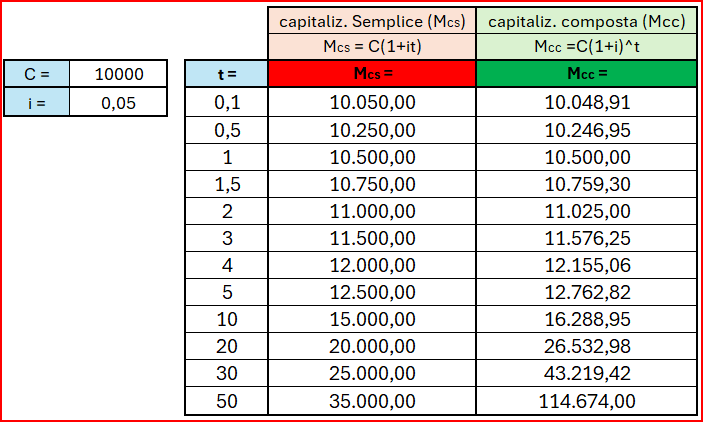
Possiamo quindi osservare che:
- Per durate inferiori ad 1 periodo di tempo t la capitalizzazione semplice genera un montante superiore
- Per durate uguali ad 1 periodo di tempo t i montanti generati dai 2 regimi di capitalizzazione si equivalgono
- Per durate superiori ad 1 periodo di tempo t la capitalizzazione composta genera un montante superiore
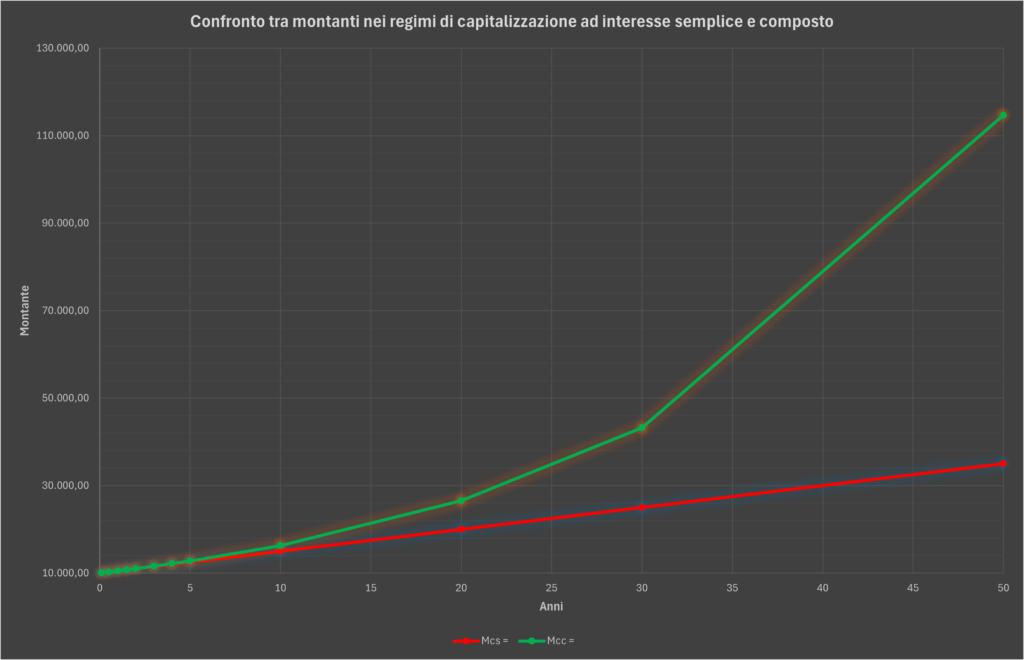
In forma grafica, il confronto tra i regimi di capitalizzazione ad interesse semplice ed interesse composto esposto nella tabella precedente risulta ancora più evidente:
Attenzione: il tasso d’interesse e l’unità di misura del tempo
Vale la stessa considerazione fatta per l’interesse semplice.
Per calcolare correttamente l’interesse I ed il montante M di ogni operazione finanziaria è fondamentale verificare che sia il tasso di interesse che la durata del tempo siano riferiti alla stessa unità di misura del tempo.
In altre parole non possiamo utilizzare un tasso di interesse i calcolato trimestralmente se il periodo di tempo t viene misurato in anni.
In questo caso occorre convertire il tempo t seguendo l’unità di misura espressa dal tasso di interesse i.
Esempio: ipotizziamo di prendere in prestito da una società finanziaria 1.000 Euro (C=1.000), al tasso di interesse semestrale dell’ 1,5% (i=0,015) per un periodo di 4 anni.
Poiché il tasso di interesse è semestrale, non possiamo utilizzare la durata t in anni. Dobbiamo prima convertire tale durata in semestri e soltanto allora potremo calcolare il montante della nostra operazione.
In questo caso poiché un anno è composto da 2 semestri, possiamo facilmente dire che t è uguale a 2 (il numero di semestri in ogni anno) moltiplicato per 4 (il numero di anni dell’operazione), ovvero 8 (t = 2 * 4 = 8)
Di conseguenza il montante dell’operazione sarà il seguente:
M = 1.000 (1 + 0,015) ^ 8 = 1000 (1,12) = 1.126,49
Conclusione
In conclusione, la capitalizzazione ad interesse composto è un concetto fondamentale nella matematica finanziaria e nella pianificazione finanziaria personale. Inoltre, l’interesse composto è alla base di molti strumenti finanziari.
Grazie alla sua capacità di generare una crescita esponenziale del capitale, l’interesse composto è uno strumento potente per massimizzare i tuoi investimenti a lungo termine. Comprendere come funziona e come applicarlo alle tue decisioni finanziarie può aiutarti a raggiungere nella pianificazione dei tuoi obiettivi finanziari di lungo periodo.
