Il regime di capitalizzazione ad interesse semplice ha due caratteristiche:
- l’interesse maturato nell’operazione finanziaria è direttamente proporzionale al capitale iniziale, alla durata dell’operazione ed al tasso di interesse
- l’interesse si rende disponibile alla fine del periodo dell’operazione finanziaria; di conseguenza si aggiunge al capitale iniziale e non genera ulteriori interessi (come invece accadrà quando analizzeremo l’interesse composto)
Cerchiamo di capire che cosa significa con l’aiuto di formule, grafici ed esempi.
Formule
Per la prima caratteristica vista precedentemente, l’interesse I maturato al tempo t è proporzionale al capitale iniziale, alla durata ed al tasso di interesse. Il che può essere riassunto con la seguente formula:
I(t) = C i t
Ma come abbiamo detto nel precedente articolo, il montante è la somma del capitale e dell’interesse:
M = C + I
Pertanto sostituendo la I nella formula del montante avremo che:
M = C + Cit
Ovvero, semplificando per il capitale C si ottiene la formula di calcolo del montante nel regime di capitalizzazione ad interesse semplice:
M = C (1 + it)
Facciamo 2 esempi. I numeri aiutano sempre a capire meglio
1- Ipotizziamo di prestare ad un amico un capitale C pari a 100 Euro (C=100), per un tempo t pari ad un anno (t=1), ad un tasso di interesse i pari all’1% annuo (i=0,01).
Sostituendo questi valori nelle formula precedenti otteniamo che:
I = 100 * 0,01 * 1 = 1
M = 100 (1 + 0,01 * 1) = 100 (1,01) = 101
2- Ipotizziamo questa volta di prestare ad un amico un capitale C pari a 1.000 Euro (C=1.000), per un periodo di tempo pari a 4 anni (t=4), ad un tasso di interesse i del 2% annuo (i=0,02).
Sostituendo questi valori nelle formula precedenti otteniamo che:
I = 1000 * 0,02 * 4 = 80
M = 1000 (1 + 0,02 * 4) = 1000 (1,08) = 1.080
Disegniamo l’interesse semplice in forma grafica
Graficamente, possiamo rappresentare l’interesse I come una retta che parte da 0 e che progressivamente nel tempo genera interessi in maniera lineare, come mostrato dalla retta I(t).
Il montante cresce anch’esso in maniera lineare come mostrato dalla retta M(t).
La distanza tra le due rette è pari al valore del capitale iniziale C.
Infatti al tempo 0 (quando inizia l’operazione finanziaria), non sono ancora stati generati interessi ed il valore del montante equivale a C, che è il punto di intersezione con l’asse verticale:
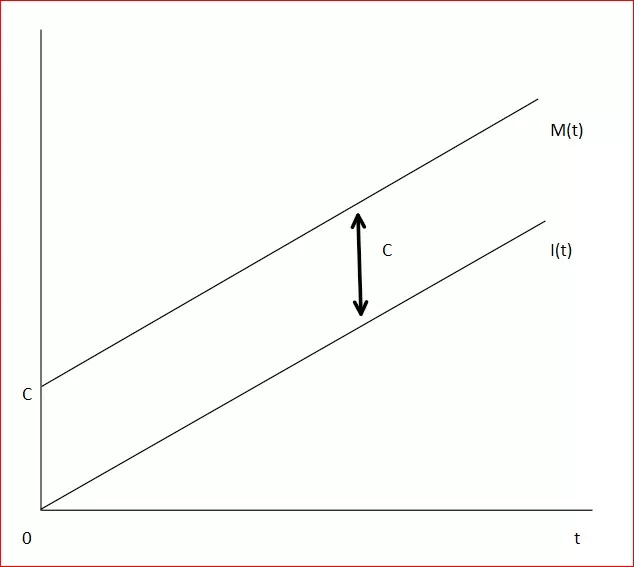
L’inclinazione delle rette dipende dal fattore di montante (ovvero la parte (1 + it) della formula usata per il calcolo del montante. Questo fattore indica la velocità con cui il capitale iniziale accresce il suo valore nel corso del tempo.
Attenzione-1: il tasso d’interesse e l’unità di misura del tempo
Per calcolare correttamente l’interesse I ed il montante M di ogni operazione finanziaria è fondamentale verificare che sia il tasso di interesse che la durata del tempo siano riferiti alla stessa unità di misura del tempo.
In altre parole non possiamo utilizzare un tasso di interesse i calcolato trimestralmente se il periodo di tempo t viene misurato in anni.
In questo caso occorre convertire il tempo t seguendo l’unità di misura espressa dal tasso di interesse i.
Esempio: ipotizziamo di prendere in prestito da una società finanziaria 1.000 Euro (C=1.000), al tasso di interesse semestrale dell’ 1,5% (i=0,015) per un periodo di 4 anni.
Poiché il tasso di interesse è semestrale, non possiamo utilizzare la durata t in anni. Dobbiamo prima convertire tale durata in semestri e soltanto allora potremo calcolare il montante della nostra operazione.
In questo caso poiché un anno è composto da 2 semestri, possiamo facilmente dire che t è uguale a 2 (il numero di semestri in ogni anno) moltiplicato per 4 (il numero di anni dell’operazione), ovvero 8 (t = 2 * 4 = 8)
Di conseguenza il montante dell’operazione sarà il seguente:
M = 1.000 (1 + 0,015 * 8) = 1000 (1,12) = 1.120
Quando si utilizza un tasso di interesse non annuale, spesso si utilizza un pedice per indicare il numero di eventi corrispondenti ad un anno di calendario, per cui avremo ad esempio i2 ad indicare un tasso semestrale (2 semestri in un anno) o i4 ad indicare un tasso trimestrale (4 trimestri in un anno).
Attenzione-2: durata (non intera) o frazionale
Potrebbe essere talvolta necessario calcolare il montante per una durata “non intera”, ad esempio un periodo di 2,5 anni o 4,3 mesi.
In questo caso non ci sono differenze nella formula di calcolo del montante, che resta sempre M = C (1 + it).
Resta sempre valida la necessità di avere durata e tasso di interessi riferiti alla medesima unità di misura del tempo (ad esempio entrambi mensili o trimestrali ecc.).
Considera inoltre che se l’unita di misura del tempo è il giorno, spesso si utilizza per convenzione un periodo di 30 giorni per un mese e 360 giorni per l’anno (anno commerciale) invece dei 365 (o 366) previsti dal calendario (anno civile)
Ancora qualche esempio
3- Ipotizziamo di prestare ad un amico un capitale C pari a 500 Euro (C=500), ad un tasso di interesse i pari al 3% semestrale (i2=0,03), per un tempo t pari a 3 mesi (t = 3 / 6 = 0,5 semestri).
Sostituendo questi valori nelle formula precedenti otteniamo che:
I = 500 * 0,03 * 0,5 = 7,5
M = 500 (1 + 0,03 * 0,5) = 500 (1,015) = 507,5
4- Ipotizziamo di compare un PC il cui costo iniziale è di 699 Euro (C=699), su cui paghiamo un tasso di interesse annuale del 4,99% (i=0,0499) dopo un periodo di 18 mesi (t =18 / 12 = 1,5).
Quale sarà il costo finale del computer, cioè il montante dell’operazione?
Sostituendo questi valori nelle formula precedenti otteniamo che:
I = 699 * 0,0499 * 1,5 = 52,32015
M = 699 (1 + 0,0499 * 1,5) = 699 (1,07485) = 751,32015
Formule inverse
In tutti gli esempi precedenti abbiamo calcolato l’interesse I (e di conseguenza il montante M) avendo C, i e t come dati. Va da sé che, qualora la variabile ignota fosse un’altra, con una semplice operazione algebrica possiamo isolarla ed andarla a risolvere. Ti riporto qui di seguito le relative formule:
- C = I / (i * t)
- i = I / (C * t)
- t = I / (C * i)
