Le rendite (2): valore attuale e montante

Nel precedente articolo abbiamo visto (in teoria) cosa sono le rendite e, sulla base delle loro caratteristiche, come si possono classificare. 

Oggi andremo un pochettino più nel pratico e vedremo, in un paio di esempi concreti, che cos’è una rendita e come possiamo calcolarne il suo valore attuale ed il montante. 

Partiamo con un esempio che mostri concretamente cos’è una rendita: abbiamo detto che si tratta di una serie di pagamenti (in ingresso o in uscita), tutti dello stesso segno. 

Ipotizziamo quindi che Giuseppe versi una rata di 1.000 Euro alla fine dei primi 2 anni, non versi nulla il terzo anno e poi versi altre 2 rate da 2.000 Euro il quarto ed il quinto anno. 

Possiamo quindi capire che si tratta di una rendita non periodica (gli importi non hanno una scadenza regolare), le cui rate sono variabili (gli importi cambiano nel tempo) e posticipate (poiché Giuseppe le versa alla fine di ciascun periodo). 

Graficamente possiamo disegnare la rendita in questa maniera: 

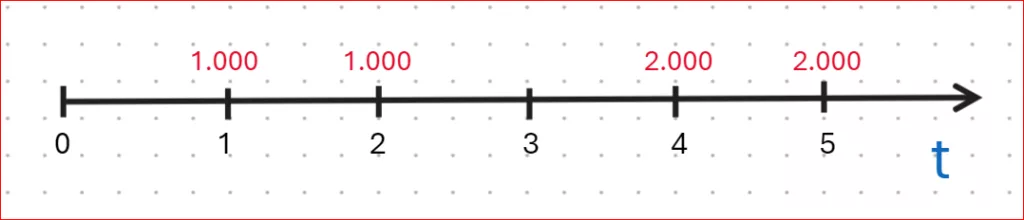
Calcolare il Valore Attuale di una rendita 

Il passo successivo sarà quello di calcolare il valore attuale questa rendita, ipotizzando di utilizzare il regime della capitalizzazione composta ed un tasso di interesse annuo del 3,25% (ovvero il tasso ufficiale della BCE sui depositi al 10/11/24). 

Il valore attuale di una rendita corrisponde alla sommatoria dei valori attuali di ciascuno dei pagamenti che compongono la rendita. Ovvero ciascuna delle rate dovrà essere attualizzata al tempo 0. 

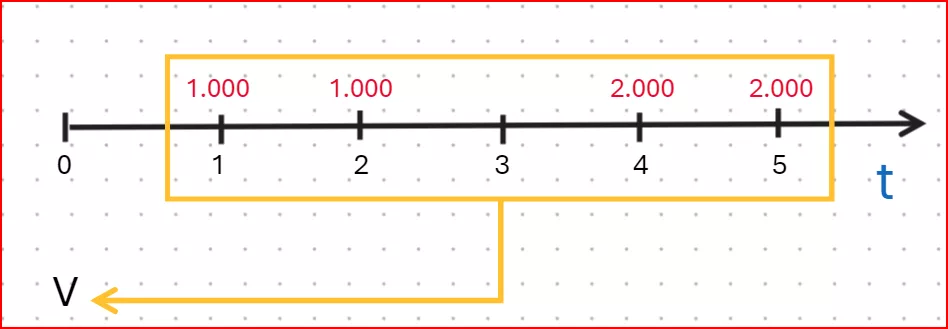
Poiché in questo esempio, parliamo di una rendita non periodica e con rate variabili, non abbiamo una formula per poterla calcolare e quindi dobbiamo calcolare separatamente il valore attuale di ciascuna delle rate. Quindi: 

V = Σ R / (1 + i ) ^t  = [(1.000 / 1,0325¹) + (1.000 / 1,0325²) + (2.000 / 1,0325⁴) + (2.000 / 1,0325⁵)] =  

          = 968,523 + 938,036 + 1.759,826 + 1.704,432 = 5.370,82 Euro 

Ovvero, privarci oggi di 5.370,82 Euro, in un mercato che rende il 3,25% annuo, corrisponde a pagarne 6.000 nel corso dei prossimi 5 anni, secondo il piano di pagamenti sopra delineato. 

Nota 1: 

Attenzione a t. Dobbiamo calcolare gli anni effettivi di attualizzazione, in base alla scadenza delle rate. Nel nostro esempio il primo anno t equivale ad 1 perché la prima rata viene pagata alla fine del primo periodo, pertanto per calcolare il valore attuale dobbiamo riportare la rata “indietro” di un periodo. Allo stesso modo la seconda rata viene attualizzata di 2 periodi mentre la terza rata di 4 (perché nel terzo anno non viene pagata alcuna rata, la terza viene pagata alla fine del quarto anno) e la quarta rata di 5 (per lo stesso motivo) 

Nota 2: 

Come già visto nei calcoli di capitalizzazione ed attualizzazione, vale sempre la regola che il tasso di interesse ed il tempo devono essere riferiti alla stessa unità di misura del tempo. Pertanto se il tasso di interesse i è un tasso trimestrale ed il tempo t è misurato in anni, dovrò moltiplicare il numero degli anni per 4, poiché in un anno ci sono 4 trimestri. 

Nota 3: 

Alcuni manuali riportano la formula di calcolo del valore attuale come fattore moltiplicativo elevato ad un t negativo, cioè: 

V = Σ R * (1 + i ) ^{– t}  

Questa formula è equivalente a quella mostrata nel calcolo precedente, potete usare quella che vi risulta più comoda. 

In pratica: 

V = Σ R / (1 + i ) ^t  = Σ R * (1 + i ) ^{– t}  

Calcolare il Montante di una rendita 

Ipotizziamo di mantenere il regime della capitalizzazione composta ed il tasso di interesse annuo del 3,25%. 

Analogamente a quanto visto prima, il montante di una rendita corrisponde alla sommatoria dei montanti di ciascuna delle rate che compongono la rendita. Ovvero ciascuna delle rate dovrà essere capitalizzata fino al momento della scadenza della rendita, ovvero a t = 5 nel nostro esempio. 

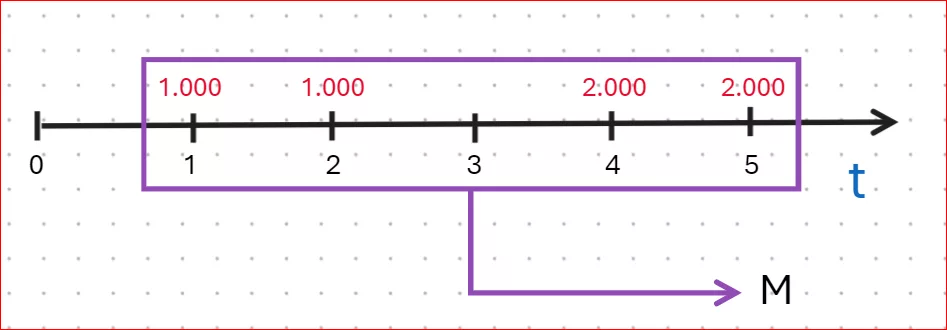
Anche in questo caso parliamo di una rendita non periodica e con rate variabili e quindi non abbiamo una formula per poterla calcolare. Dobbiamo calcolare separatamente il montante di ciascuna delle rate. Quindi: 

M = Σ R * (1 + i ) ^t  =  [(1000 * 1,0325)⁴ + (1000 * 1,0325)³ + (2000 * 1,0325)¹ + 2000] =  

= 1.136,475 + 1.100,703 + 2065 + 2000 = 6.302,18 Euro 

Ovvero, investire 6.000 Euro in un mercato che rende il 3,25% annuo, con pagamenti scadenzati come previsto nell’esercizio, corrisponde a averne a disposizione 6.302,18 tra 5 anni. 

Nota 1: 

Attenzione a t. Dobbiamo calcolare gli anni effettivi di capitalizzazione. Nel nostro esempio t equivale a 5, che è la durata della rendita, ma non tutte le rate devono essere capitalizzate per 5 anni. La prima rata viene pagata nel periodo 1 e quindi deve essere capitalizzata per 4 anni, per poterne calcolare il valore al quinto anno (5-1). Analogamente la seconda rata, pagata in anno 2, deve essere capitalizzata per 3 anni per arrivare alla fine della rendita. Di conseguenza la rata 3, che viene corrisposta alla fine del quarto anno deve essere capitalizzata per un solo periodo mentre l’ultima rata viene pagata al momento in cui si conclude la rendita (anno 5) e pertanto non necessita di alcuna capitalizzazione. 

Nota 2: 

Come già visto nei calcoli di capitalizzazione ed attualizzazione, vale sempre la regola che il tasso di interesse ed il tempo devono essere riferiti alla stessa unità di misura del tempo. Pertanto se il tasso di interesse i è un tasso semestrale ed il tempo t è misurato in anni, dovrò moltiplicare il numero degli anni per 2, poiché in un anno ci sono 2 semestri. 

Nei prossimi articoli vedremo alcuni casi particolari di rendita, nei quali calcoleremo il valore attuale ed il montante utilizzando delle formule, senza la necessità di calcolare il V o il M di ogni singola rata.