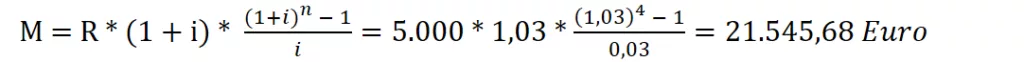Come visto nel precedente articolo, per calcolare il valore attuale ed il montante di una rendita dobbiamo calcolare il valore attuale ed il montante di ciascuna rata che la compone.
Esistono però dei casi particolari in cui è possibile usare delle formule che ci permettono di calcolare valore attuale e montante in maniera molto più semplice. Questo accade ad esempio quando le rate sono tutte dello stesso importo ed equamente distribuite nel tempo. Vediamo insieme alcuni esempi, in cui utilizzeremo sempre il regime dell’interesse composto.
Rendita periodica immediata posticipata di n rate costanti di importo R
Questa rendita, che inizia “immediatamente” al tempo 0, si caratterizza per avere n rate periodiche (ad esempio annuali) costanti di importo R che vengono pagate alla fine di ciascun periodo (ovvero la prima rata viene pagata alla fine del primo periodo annuale), capitalizzate secondo un tasso di interesse i.
Ipotizziamo uno scenario in cui Enzo versa alla fine di ogni anno, per 4 anni, una rata di 5.000 Euro in un fondo obbligazionario che rende il 3% annuo.
Quindi:
R = 5.000 Euro ; n = 4 ; i = 0,03 .
Valore attuale:
Il valore attuale V si calcola secondo questa formula:
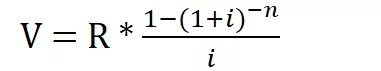
Dove il fattore moltiplicativo di R:
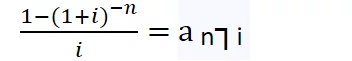
a n┐i che si legge “a figurato n al tasso i” permette di attualizzare ogni singola rata della rendita al periodo antecedente il pagamento della prima rata (t = 0 in questo caso) e corrisponde al valore attuale nel caso di rendita unitaria (cioè con R = 1).
Graficamente possiamo rappresentare questa rendita in questa maniera:
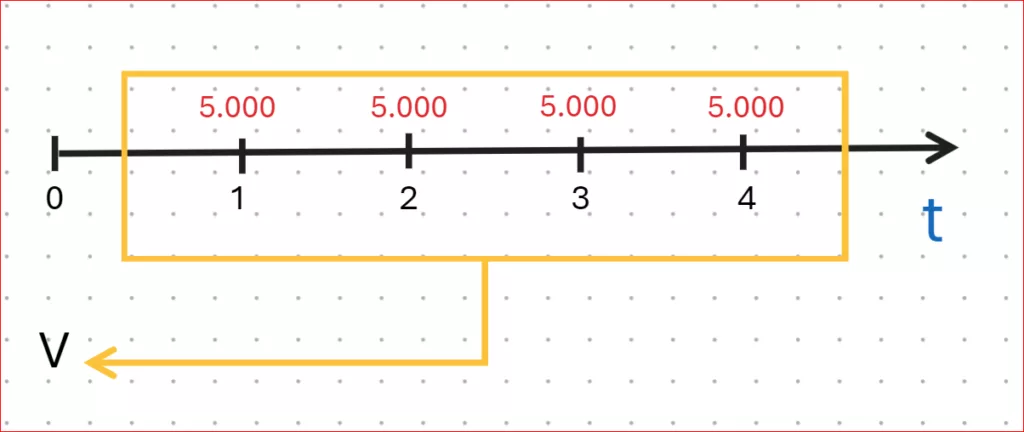
Calcoliamo il valore attuale di tale rendita, usando i dati e le formule sopra riportate:
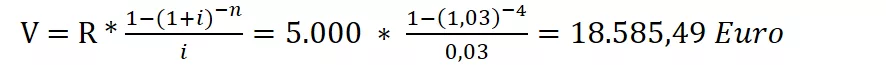
Montante
Il montante M si calcola secondo questa formula:
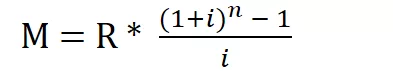
Dove il fattore moltiplicativo di R:
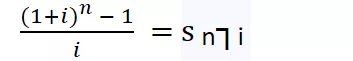
s n┐i che si legge “s figurato n al tasso i” permette di capitalizzare fino al momento dell’ultima rata (la quale, scadendo alla fine della rendita non necessita di capitalizzazione) e corrisponde al montante nel caso di rendita unitaria (cioè con R =1).
Graficamente possiamo rappresentare questa rendita in questa maniera:
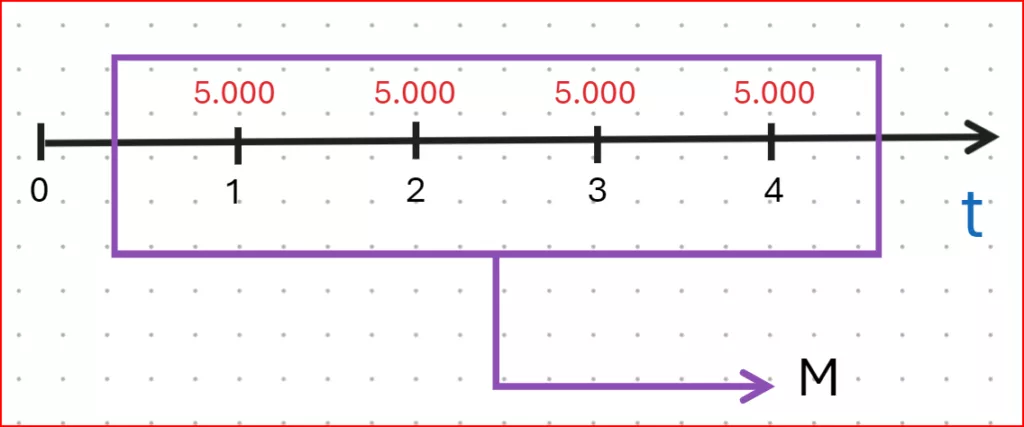
Calcoliamo il montante di tale rendita, usando i dati e la formule sopra riportate:
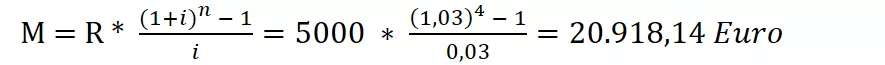
Rendita periodica immediata anticipata di n rate costanti di importo R
Questa rendita, che inizia “immediatamente” al tempo 0, si caratterizza per avere n rate periodiche (ad esempio annuali) costanti di importo R che vengono pagate all’inizio di ciascun periodo (ovvero la prima rata viene pagata al tempo 0, appena la rendita comincia), capitalizzate secondo un tasso di interesse i.
Ipotizziamo uno scenario in cui Pinuccio versa all’inizio di ogni anno, per 4 anni, una rata di 5.000 Euro in un fondo obbligazionario che rende il 3% annuo.
Quindi:
R = 5.000 Euro ; n = 4 ; i = 0,03 .
Valore attuale:
Il valore attuale V si calcola secondo questa formula:
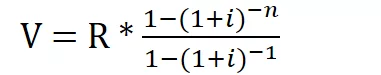
Dove il fattore moltiplicativo di R:
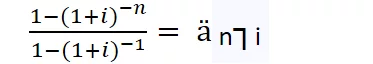
ä n┐i che si legge “a anticipato figurato n al tasso i” permette di attualizzare ogni singola rata della rendita al periodo antecedente il pagamento della prima rata (t = 0 in questo caso) e corrisponde al valore attuale nel caso di rendita unitaria (cioè con R = 1)
Graficamente possiamo rappresentare questa rendita in questa maniera:
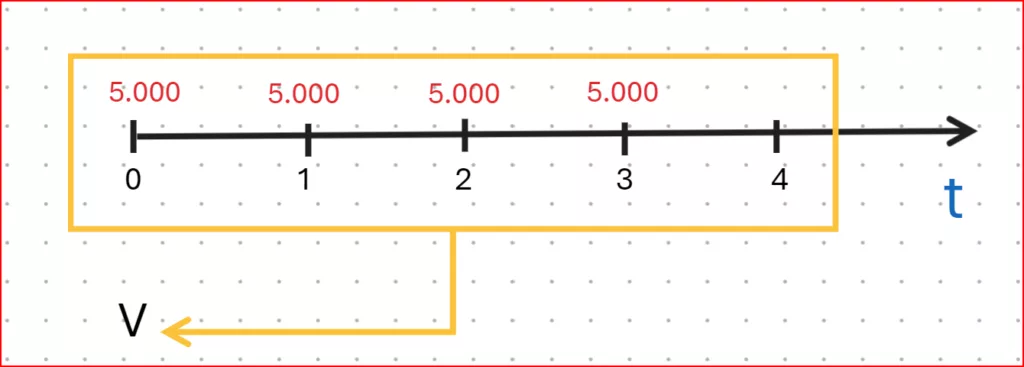
Calcoliamo il valore attuale di tale rendita, usando i dati e le formule sopra riportate:
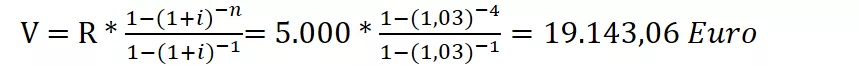
Montante
Il montante M si calcola secondo questa formula:
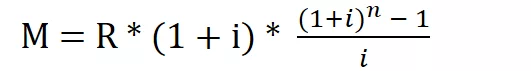
Dove il fattore moltiplicativo di R:
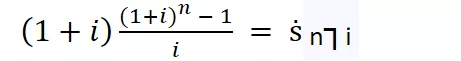
ṡ n┐i che si legge “s anticipato figurato n al tasso i” permette di permette di capitalizzare fino al momento dell’ultima rata (la quale, scadendo all’inizio dell’ultimo periodo necessita di un periodo di capitalizzazione) e corrisponde al montante nel caso di rendita unitaria (cioè con R =1).
Graficamente possiamo rappresentare questa rendita in questa maniera:
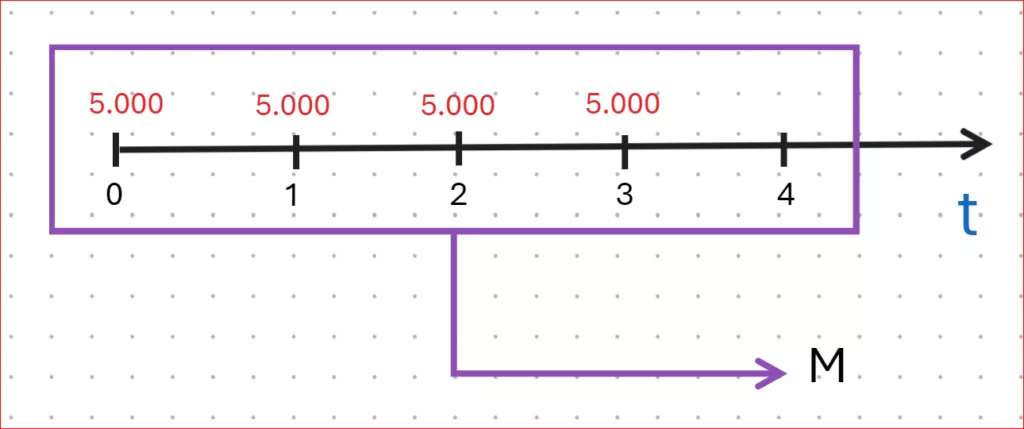
Calcoliamo il montante di tale rendita, usando i dati e la formule sopra riportate: